Linear Algebra: Parametric Representation of Lines

Linear Algebra: Parametric Representation of a Line

Lines in 2-d space can be represented by $y=mx+b$, but with higher dimensional spaces it can help to generalize the formula for a line. If we have $\overrightarrow{a}$, we can define a set $S=\left\{c\ast \overrightarrow{a}|c\in ℝ\right\}$. Taking all real numbers and multiplying them by our vector give us a set of vectors that span the line of $\overrightarrow{a}$. This set notation can be used to create a line from a vector of any dimension.

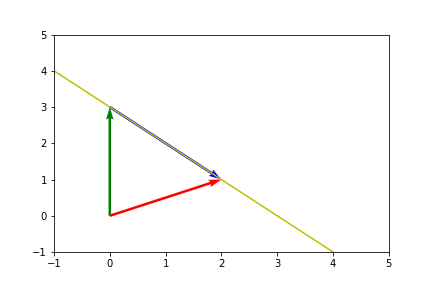
Linear Algebra: Defining Parallel Lines

Defining a parallel line becomes simple, especially when dealing with many dimensions where ”slope” isn’t intuitive. Let’s say we have $\overrightarrow{a}=\left(2,1\right)$,$\overrightarrow{b}=\left(0,3\right)$ and we want a parallel line from $S=\left\{c\ast \overrightarrow{a}|c\in ℝ\right\}$ that passes through the point defined by $\overrightarrow{b}$. What we can do is take our set $S$ and modify it to be the parallel line $P=\left\{\overrightarrow{b}+t\ast \overrightarrow{a}|t\in ℝ\right\}$. This is taking all the point defined on our line by $S$, and offsetting them by $\overrightarrow{b}$ over to a parallel line that passes through $\overrightarrow{b}$, as seen in the graph below. This definition extends to vectors of any dimension.

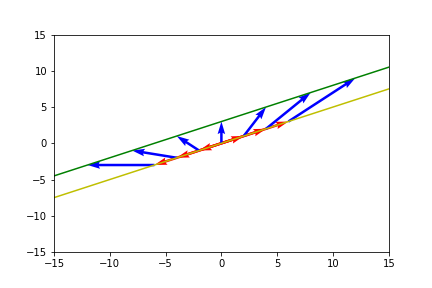
Linear Algebra: Defining Lines through 2 Vectors

Defining a line that passes through the endpoints of 2 vectors is also simple with our set definition of a line. All we need is to translate either $\overrightarrow{a}$ or $\overrightarrow{b}$ by all the points on the line defined by $\overrightarrow{a}-\overrightarrow{b}$, which is just the vector between their endpoints. Formula is $L=\left\{\overrightarrow{a}+t\left(\overrightarrow{a}-\overrightarrow{b}\right)|t\in ℝ\right\}$.